Drawing on the Hyperanalytical Side of the Brain

1. Introduction

What's the deal with drawing? Why's it so hard for most people? By 'drawing' I specifically mean an attempt to reproduce on paper some thing or image that's actually in front of you.

Way back when I had a serious interest in drawing; the most important and useful book I ever read on the subject is called Drawing on the Right Side of the Brain, by Betty Edwards. Its basic point is that most of us are hobbled in our attempts to draw by our persistent tendency to overcode visual information with symbolic meaning; doing so causes us to draw our symbols rather than what we are actually seeing. Realizing and addressing this can quickly and profoundly improve people's ability to draw; I've seen it happen to a friend who was hopeless before reading the book.

Of course, an artist's technical development can hardly end there; what's the next step? Making our drawings more accurate, presumably. Is this just a matter of practice, transcribing shape after shape until our basic ability to perceive lengths, angles, and ratios is finely honed? No. I believe that becoming proficient at drawing has more to do with the strategic management of error (analogous to error management in scientific computing) than with the elimination of one's basic susceptibility to error.

I don't think this is a novel or controversial thesis. Furthermore, plenty of books, like Edwards', will teach you various ways to do this better than I could. So why am I writing this? I want to propose an analytical model of the activity of drawing that will give a precise (albeit idealized) account of error and justify techniques of error-management. I hope this model might make the act of drawing seem more interesting and approachable to the sort of people who might stumble on this blog in the first place.

Of course, great drawings involve a connection between artist and subject that goes beyond simple fidelity to its spatial proportions. However, I hope to convince readers that even achieving spatial accuracy is a richly complex activity. The artist is not just a passive photocopier of reality, but must perceive the high-level structure of an image and plan her drawing accordingly.

Warning: I'm a barely-competent artist with no knowledge of the current state of drawing research. You should probably stop reading now.

2. Working Assumptions and Model Criteria

Here are my starting points for the model, which will use a modest amount of mathematics.

1. The target image, i.e. the thing the artist wants to reproduce, is a finite set of points (p[1], ... p[n]) in the x-y plane (the target plane). The drawn image is another set of points (called marks, labeled m[1], ... m[n]) in another x-y plane (the drawing plane, initially empty), each with an intended correspondent in the target plane.

Obviously, this is purely a modelling assumption and reflects no conviction about 'the way things are'. I don't think that the visual field is truly describable as an x-y plane; I'm arbitrarily suppressing questions of 3-D rendering by assuming a flat target; and I'm throwing out lines, shading, color, etc.

2. Drawing is sequential; one point at a time. Moreover, drawing is local. By this I mean that, in determining the location of the next mark, the artist consults only a 'small' number of previously drawn marks, along with their corresponding points. I think this assumption can be falsified, but generally it's too taxing to bring very much information usefully to bear in the production of a single mark.

3. Each mark-making action is error-prone (stochastic, if you like). For simplicity, rather than a probability distribution, I will assume a possibility set of possible positions for a new mark that's a function of the positions of the marks and points taken into consideration by the artist's local rule.

4. Error is scale-invariant. That is, if we shrink or grow the target image, holding proportions fixed, the possibility-sets for new marks will not be affected. This reflects the experience that shifting one's distance from a drawn object does not reliably make for a better drawing (assuming the object wasn't too close or too far away to be clearly perceptible).

Similarly, if we shrink or grow the drawn image-so-far, the possibility-sets for new marks will shrink or grow proportionally. (If error was an absolute quantity, e.g. the drawn point would fall at most an absolute distance e from the correct point, we could all just make very large drawings and the errors would become insignificant flaws on an essentially-perfect rendering. Alas, it doesn't work that way. Now, the implausibility of the absolute-error model doesn't prove the scale-invariant model--there's probably a more nuanced alternative--but I'm going to go with it.)

5. More reference points are useful in determining a new mark. Example: you are given the target image on the left, and have marked A' and B' on the drawing plane (not quite to scale, but that's OK as long as you get C' placed accordingly).
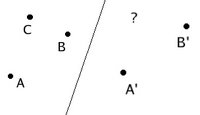Now you've got to mark C'. My contention is simply that having both A' and B' already placed makes it easier to place C' well; you can check the new mark's relation to two points instead of just one. Of course, it takes at least two reference points just to get a sense of the scale being used in the drawing; but beyond that, there is also additional helpful angular information.

3. The Model

OK, here is a model that I believe honors 1 thru 5 above. 1 and 2 are obeyed verbatim. I don't directly in the model describe how the artist chooses which mark to make next, or which reference points to use in making it (since my main goal is to suggest strategies for making such choices). Therefore, the remaining task is to define how the possibility-sets for new mark location are formed.

First, the artist has two underlying accuracy parameters which we'll call theta and epsilon. Lower values will mean greater accuracy; the first parameter relates to angular accuracy, the second to distance accuracy.

The artist chooses a length-reference pair m[i], m[j], of distinct marks from those already made. The presumptive size-inflation factor of the drawn image relative to the target is then estimated as the ratio of lengths R = L'/L, where L is the distance from p[i] to p[j] and L' is the distance from m[i] to m[j].

This value R is not consciously available to the artist (that's exactly the kind of precision we don't possess); rather, it helps determine the possibility-set for the new mark m[k], as we will describe.

For each additional reference point m[l], a constraint C[l] is placed on the possibility-set (so, more reference points mean less room for error). C[l] has two components. The first one, the length constraint, states that the distance from m[l] to m[k] must be between R*(1 - epsilon)*D and R*(1 + epsilon)*D, where D is the distance from p[l] to p[k].

(Note: I think that this constraint actually becomes tighter when D is approximately L; that is, it's easier to copy a length than it is to scale it up or down. But I won't model this.)

The second component, the angular constraint, states that the vector connecting m[l] to m[k] must form an angle A' with the horizontal that differs by at most theta from the angle A formed with the horizontal by the vector connecting p[l] to p[k].

Thus each such reference point m[l] poses a constraint that looks like the following (C[l] forces m[k] to be placed in the shaded region):
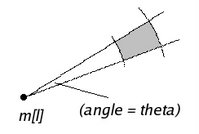This completes the description of the model. There is only one technicality: what if the constraints cannot all be satisfied? This is a sign that something is wrong with the drawn image, since a fully faithful partially drawn image (at any scale) will always impose constraints satisfied by the 'perfect' marks which complete the drawing, no matter which reference points are chosen. Maybe an inconsistency causes the artist to start over, or pick a mark position satisfying as many constraints as possible.

4. Drawing Strategies Suggested by the Model

In what follows, I'm going to assume that the technicality just mentioned never arises.

1. When possible, choose orthogonal reference points.
Notice that if two such reference points are chosen that lie very close together (both in the target and drawn images), they will impose nearly identical constraints and be functionally redundant, whereas reference points forming a larger angle with the point to be drawn cut down more on wiggle-room, as depicted below.
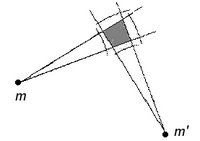If the constraint regions were circular, rather than slices of an annulus, this effect wouldn't appear; one constraint region would be contained in all the others, and the corresponding reference point would subsume the usefulness of all the others. This would be a violation of assumption 5, and contrary to my general experience.

2. When possible, choose reference points that are close to the point to be drawn (on the image plane).
For, the shaded area of the constraints we described grows directly as the distance to the reference point increases, giving more wiggle-room for error.

Take a target image like this one of two faces (using lines for ease of illustration):

Suppose you've accurately copied the first face and want to start on the second. It seems clear that using the first face as sole reference point for drawing each of the features on the second face would be foolish; the difficulty in assessing the length of the gap between the faces would give a result like this:

You don't see too many drawings like this one. I think the close-reference-points strategy is intuitively understood by even inexperienced artists. In fact, they cling to it (perhaps also because it involves less eye movement). However, it is problematic as an exclusive strategy, and understanding why is at the core of what I want to impart about managing error in drawing.

3. Maintain a 'confidence' model of the drawn points; when possible use reference points with high confidence.

Suppose you've got the two faces drawn correctly. Say now the target image is altered to include two arms:
(I realize arms don't grow out of people's heads.)
The question is, how should we add in the arms to our drawing? Let's consider two options. First option: draw the leftmost arm, starting from the left face, up to its point of contact with the right arm, then continue the right arm down to the left face.
Second option: draw the left and right arms separately in turn out from their faces, meeting the two in the middle.

In either case we allow any previously drawn marks to serve as reference points. In both cases, except for the discontinuity of switching arms in executing the second option, the dominant (because tightest) constraints are consistently provided by the portions of arm just drawn (these are the closest to the marks about to be made).

As an arm being drawn 'grows' outward from its head, under our model the possible absolute distance of each drawn point from its 'correct' point (relative to the faithfully drawn heads) grows as at least epsilon times the distance to the head from which the arm is growing. This suggests that we should prefer the second drawing option; in fact, since the left arm is longer, we should probably grow part of the left hand out of the right hand--this minimizes the maximum distance from any point-to-be-drawn from its reference 'source' on the two heads.

4. Watch out for error-accumulation in reference lengths; use confidence models here as well.

The importance of using confident reference points is heightened by the fact that error can accumulate in length-reference pairs as well. Inexperienced artists, when drawing a feature in a vicinity of their picture, over-rely on that vicinity to determine scale as well as relative position. So, if features have gotten too enlarged in a picture region (typically an 'interesting' region with lots of detail), they will continue to be drawn overly large thereabouts because the length-reference pairs will be chosen locally.

Note that in the discussion of the arm-drawing, we strategically chose not only reference points, but also which points we were to draw next. So, generalizing:

5. Choose points to be drawn next that have close, orthogonal, and/or confident reference points available.

All these goals may conflict, and need to be weighted in decision-making. I don't think I could say anything quantitive here that would be of much value.

There is one issue we skirted over. In drawing the arms, we assumed we had two distant and accurate reference points (the two heads). What reason do we have to assume this? Well, the first large length we draw can be nominated as the governing scale factor for our drawing, i.e. presumed accurate; but beyond this we necessarily face significant error in drawing points at significant distances.

I think the most honest account of how this is to be overcome is to admit that our accuracy is a parameter that varies with effort.

5. When 1-5 are inapplicable or insufficient, use more effort.

A good drawing begins with a modest number of key reference points being drawn with high effort and high accuracy; these points are chosen to 'cover' pictorial space, so that the remaining points are each reasonably close to one of the key points. The key points each then serve as the seeds of 'arborescences' of new, close points which depend on the accuracy of the initial points from which they grow (the artist may also put down secondary and tertiary layers of less-key reference points, giving a finer cover to work with); these later stages of the drawing require less strict accuracy because they are less relied-upon. In summary:

6. Draw with a plan.

Visualize ahead of time the reference-point dependencies to be used among the points that need drawing. Aim for this dependency graph to be shallow, with individual points backed up either with effort or with good (confident, close, orthogonal) reference points. Since there is an initial paucity of reference points, intelligently applied initial effort plays an important role for the drawing, as described in the previous paragraph.


That's all I've got! Of course, I would love feedback from anyone, experienced artist or otherwise.

Trees and Infinity

With this post I hope to do a little to strengthen readers' (and my) understanding of the mathematics of the infinite (something easy to neglect in the study of resource-bounded computation), while focusing on the discrete infinite structures that arise in computability theory.

In mathematics, a tree is an important kind of structure. It consists of a set of nodes, with one designated the root. Each node has a (possibly empty) set of 'children' (of which it is the parent), and any node is reachable from the root in a unique way by a finite series of steps, where each step takes you from a node to one of its children.

The genealogies of asexual organisms, for example, are naturally describable using trees. An important tree in discrete math is that formed with the finite bitstrings as nodes, where the root is the empty string and where the children of x are x0 and x1. (Exercise: use this tree to exhibit the following, somewhat startling, phenomenon: there exists an uncountable collection of subsets of N, the natural numbers, such that any two subsets have at most a finite intersection.)

This tree on bitstrings is an infinite tree, but it has the nice property of being 'locally finite': every node has only finitely many children. Konig's Lemma (the 'o' in Konig needs an umlaut) asserts that any infinite, locally finite tree contains an infinite path (hopping parent-to-child at each step).

The proof is simple: we build such a path. Start at the root; by the pigeonhole principle, one of the root's children c must itself be the root of an infinite subtree. Hop to c, repeat the same process, ad infinitum.
QED.

This innocuous Lemma is in fact very powerful. I will describe some basic applications.

1) The Compactness Theorem for Propositional Logic: Suppose {F_i} is an infinite family of Boolean functions over x_1, x_2, ..., such that i) each F_i depends on finitely many variables, ii) for each K we can find a setting of the variables that satisfies F_1, F_2, ... F_k (i.e. makes them all equal 1).
Then we can find an assignment satisfying all the F_i simultaneously.

Proof: For any finite bitstring y, say of length j, interpret y as an assignment to x_1, ... x_j. Say y is in T if there is no particular F_i that y has already forced to output 0.

T is clearly a tree, and locally finite. If it has an infinite path, that path describes an assignment satisfying all of {F_i}. So assume it does not. But then, by the contrapositive form of Konig's Lemma, T must be finite, say with no node representing a bitstring of length K or more.

This means that for any length-K bitstring y, there is some formula F_{i[y]} forced to be 0 by setting x_1 ... x_K = y.

How, then, can one find any assignment to x_1, x_2, ... that satisfies all of the finite set of formulas {F_{i[y]}: |y| = K } ? One cannot. This contradicts the assumptions of the Theorem, completing the proof.
QED.

Here's a nice application of the Compactness Theorem:

2) show that the 4-color Theorem of graph theory holds even for infinite planar graphs, as long as each graph node is of finite degree. (Assume the finite 4-color Theorem is valid. Or, hey, don't...)

Konig's Lemma or The Compactness Theorem can each yield a simple proof (exercise!) of the following 'query complexity'-type result:

3) Suppose f is a Boolean function on x = x_1, x_2, ... Say whenever f(x) = b, for b = 0 or 1, there is a finite subset of the variables which force f to equal b.
Then f in fact only depends on finitely many variables.

This result is redolent of the statement 'REC = RE intersect coRE' in computability. It also has an analogue in a more finite setting--a kind of moral equivalent of 'P = NP intersect coNP' in query complexity--which I invite readers to discover or ask about.

It's interesting to wonder to what extent Konig's Lemma can be 'constructivized'. Let D be an infinite subtree of the prefix-tree over finite strings (as described above). Suppose membership in D is computable. Say infinite string s refines D if all of its finite prefixes are in D.

4) Is it necessarily the case that for such D there is a computable s refining D? (Hint: Diagonalize.)

4.5) If the sequence of functions from the Compactness Theorem (1) is a computable one, is there a computable assignment to x_1, x_2, ... satisfying every function?

5) What if, in 4, there is an additional guarantee that only countably many s refine D?

For readers interested in Kolmogorov complexity, the following somewhat challenging result rewards similar tree thinking:

6) Suppose that for some infinite string s there is a constant C such that for all n, there is a Turing machine M_n which, on input n, outputs the length-n prefix of s.
Then s is computable. (The converse is easy.)
(Source for 6: the gorgeous Li-Vitanyi book on Kolmogorov complexity.)

Addendum: I just found a good source for further material related to 4-5 and other aspects of 'recursive (infinite) combinatorics': Bill Gasarch's chapter in the hefty Handbook of Recursive Mathematics, Vol. II.

Shifting quite a bit now, I'd like to briefly describe a nice probabilistic result about infinite genealogical trees. Consider an idealized asexual organism in an idealized environment. Each individual alive at time t (an integer) gives birth to some number (possibly zero) of offspring, whose number is determined by the outcome of a random variable X. Then the individual dies as we enter time t+1. Each new individual's reproduction is governed by the outcome of an independent copy of X (so, just because your parent had reproductive success doesn't make you more likely to).

X could be very complicated. But it turns out that the expectation E(X) is still quite powerful in understanding the population dynamics: if E(X) is less than 1 then an eventual extinction occurs with probability 1, while if E(X) is greater than 1 then extinction happens with probability less then 1, and conditioning on the event that extinction does not occur, then with probability 1 the population size goes to infinity rather than oscillating indefinitely.
The proofs I've seen of these results are generatingfunctionological. Are there more 'natural' proofs out there? Or a relation to Konig's Lemma?


I should note that real trees are worth thinking about too. I would recommend the site Carbonfund.org as what seems to be the most well-run and cost-effective place to buy carbon credits, reducing global warming and deforestation. $55 will offset 10 tons of CO2, a significant chunk of the direct yearly impact of an average American.
P.S. Anyone who uses PayPal for this kind of thing should be aware of the fraudulent emails sent by PayPal impersonators to solicit credit card numbers.

Finally, for a more soulful/whimsical take on trees and the infinite you might check out Calvino's novel The Baron in the Trees. (Thanks, Chaya!)

Theory and Me

Recently Columbia U. Press published a large anthology of literary criticism and metacriticism with the provocative title Theory's Empire. It aims to describe, from a fairly critical standpoint, the trajectories of various influential 'isms' in the recent study of literature: postcolonialism, postmodernism, deconstructionism, etc. I haven't read it yet, but judging from the blog-buzz it could be an important retrospective. I hope that some scientists too are persuaded to look it over and learn something (by way of comparison) about the vicissitudes of theory in humanities departments.

What is it that makes 'theory' so enticing? I think it can simultaneously convey feelings of surprise, hidden connections, and newfound mastery that together bring the theorist or reader into a charmed state. Thinking becomes an urgent activity, and big thoughts make contact with the world, resonating in the air like gongs.

Anyway, this was my experience as a junior and senior in high school when I discovered and got feverishly involved in the 'postmodern' theorists--Foucault, Deleuze, Baudrillard, etc. At a point when I was still fairly uninterested in math/science, tired of school, and resentful of the authority of both, these authors offered an exhilerating counternarrative and an alternative standard of intellectual rigor. Although they generally disavowed systematic thinking, their writing was characterized by a small number of patterns (often taking the form of a surprise inversion) that operated repeatedly in diverse settings to yield radical consequences--a set of 'magic keys' to experience.

That experience gradually turned sour. I realized that in my eagerness to apply these new theoretical ideas anywhere and everywhere I was becoming insensitive to the world; my thinking was driven by the need for radical contrarianism rather than the desire to truly understand. Then, too, I took my first computer science course, which opened up a whole new chapter in my adventures in theory (a tale for another time). Today I am very far removed from the person I was in that period. My relationship to theory has cooled down considerably even as it's grown happier and more productive; this is, I'm sure, due both to the nature of mathematics as a field and to my changing temperment as I leave adolescence behind (of course, the factors are related).

But mathematical and scientific theories are not necessarily so different from others. They too can form empires in our minds and govern our search for meaning, and it is up to scientists to choose their masters wisely. Just as philosophical systems like postmodernism run the risk of becoming vacuous in their generality and predetermined in their findings, I think there are significant risks in becoming absorbed in scientific trends, like 'nonlinear science', that combine emotional resonance, polemicism, and seemingly unbounded applicability.

Not to say that good science doesn't appear under that rubric. None of this should be taken as criticism of particular theories, in particular of the pomo theorists mentioned, whom I've seldom read since high school (oh yeah, and their appeal wore off even faster once I got to Swarthmore and they became commonplace..). I'm just describing an individual relationship to theory, in the hopes that it might help others reflect on theirs.

Some people have 'break-up songs', that help them both to look back and to move forward; for me and postmodernism I'd say it was Pynchon's novel 'The Crying of Lot 49', which captured in transmuted fashion a lot about my own search for meaning in high school: the growing uncanniness, the thrill of transgression and revelation; the need (without clear motive) to uncover patterns of power, domination, and covert resistance; the eventual nausea and disillusionment, along with an unshakeable sense that a mystery has slipped thru one's fingers.

And on that note--new Pynchon out this month. Fingers crossed!